Tremor along the Dead Sea Transform remotely caused by the 2023 MW7.6 Kahramanmaraş earthquake

Identification of tremor and its location via envelope cross-correlation

I restricted the analysis to data recorded by accelerometers because broadband velocity seismograms over the TRUAA network were clipped during the surface wave train. I calculate envelopes by integrating with velocity, band-pass filtering between 8 to 16 Hz, squaring, summing the three components, and smoothing with an average window running for 2 seconds.

In contrast to previous reports of evoked tremor, which contain multiple visible bursts, only two of the reported evoked tremor bursts had an SNR clearly higher than one. However, the Jordan Valley tremor is monitored using accelerometers, which are not ideal for detecting weak seismic movements. Thus, SNR levels during MW7.6 encoding allow detection of relatively strong bursts, while other bursts of smaller amplitude may be below the noise level. Note that the curvature of the motion of the first burst (205 s; Fig. 2b) is slightly stronger than that of the second burst (220 s; Fig. 2b), indicating that the first source is slightly shallower than the second. I focus on the second aftershock burst recorded in the HMDT around 220 s after the MW7.6 origin time, since its signal-to-noise ratio (SNR) is higher than that of the first aftershock burst.

The cross-correlation between two envelopes is calculated after shifting the traces according to a pre-calculated schedule. I assume a uniform S-wave speed of 3 km/s and a constant depth, and calculate travel times from a grid of possible source locations separated by 2 km in the north-south, east-west directions to each of the locations. stations. I then transfer all the traces related to the reference stations, calculate the cross-correlation, and stack them. I repeat this process after changing the source depth, correlating the source location with the grid point where the stacked cross-correlation is maximum. Maps showing stacked cross-correlations as a function of tremor and earthquake source location for different source depths are shown in Figures S1 and S2, respectively.

The small number of tremor bursts associated with the peak amplitude of the love wave raises suspicions that these signals may be misidentified. The tremor signal is of low amplitude, and its duration and frequency content may sometimes resemble those associated with man-made signals evoked by freight trains and trucks. The Jordan Valley is a sparsely traveled area with no trains, so the signal is unlikely to be due to train or truck traffic. However, the area contains a number of active quarries that regularly use explosives for mining purposes, thus producing explosions that are well recorded throughout the network. These explosions occur sometime around the same hours as the tremor identified here (12 a.m. local time). However, for the reasons stated below, I consider the possibility that the signals reported here were caused by a quarry explosion to be unlikely. First, the detected signal coincided twice with the maximum amplitudes of the love wave within 15 s. Second, the signal can be correlated between distant accelerometers tens of kilometers apart. Third, the signal locations are more consistent with a deep source than with a shallow source, in an area devoid of known active quarries. Subsequently, the spectra of the recorded query bursts differ significantly from the signal spectra that I associate with a deep tectonic earthquake. In light of these observations, I conclude that the signals reported here were excited by a tectonic source. In the section “Spectral Characteristics of Ground Motion of Triggered Tremor” I show that the large differences between the temporal and spectral features of these tremor signals to the features of local seismograms of microearthquakes also rule out the possibility that the signals I identify as tremors are actually caused by local, spot-triggered earthquakes.

Seismic images from the nearest stations GNNR and IZRL show two earthquakes occurring immediately in the Jezreel Valley. These are likely small-scale earthquakes also caused by love waves, but they are too weak to be precisely located. The excited seismic signal at station CVYN was preceded by two strong precursors (indicated by question marks in Fig. 2c,d), however, their timing and amplitude suggest that they are probably not related to the precursors recorded at GNNR, and further attempts have not been made to reveal their origin.

Spectroscopic analysis

1.5 s tremor spectra were calculated from windows with 50% overlap including 10 s of strongest tremor, averaged over the three components. Spectra are calculated using the multi-taper spectral approach. For the DST earthquake, integrated accelerations from the IS network were used starting on February 6, 2023, at 10:28:2751. For the Parkfield earthquake, I use seismograms recorded at well stations from the PB and BP networks starting on January 13, 2007, at 04:49:47 UTC52,53,54. For the Anza earthquake, I use seismograms from the AZ Network starting on 3 November 2002, at 22:34:04 UTC 55. For the Hikurangi, New Zealand earthquake, I use seismograms from the New Zealand Network starting on 27 February 2010, at 07:12: 35 UTC 56.

To find the best fitting value of the spectral decay parameter n, I assume that the tremor and surface wave signals are uncorrelated (i.e. the sum of their strengths constructively). I model the observed ground velocity power spectral density (PSD) from 4 to 13 Hz as a sum:

$${\left\vert \dot{u}(f)\right\vert}^{2}={\left\vert{A{f}^{n}}\right\vert}^{2}+ {\left\vert N(f)\right\vert }^{2},$$

(2)

where A is a fitting parameter, and N(f) is the ground velocity noise in the window preceding the arrival of the tremor (see Fig. 3a, b). I find the value of the coefficients A and n by minimizing the differences between the right and left side of equation (2). The results are shown in Figure S3. The most appropriate value of n for the HMRA and RGMN velocity spectra is 1.99 and 2.05, respectively. Integrating from velocity to displacement is equivalent to differentiating the spectra. Thus, the displacement spectra are approximately inversely proportional to the cubic frequency for both of these spectra.

Dynamic deformation gradients

The velocity gradient is calculated by taking the differences between the particle velocity measured at adjacent stations. If stations i and j are separated by a distance measured along the l direction, then the k component of the velocity gradient is given by:

$$\dot {{u}_{k,l}} = \frac {{\dot {u}}_{k}^{j} – {\dot {u}}_{k}^{i} } {{{\Delta }}l},$$

(3)

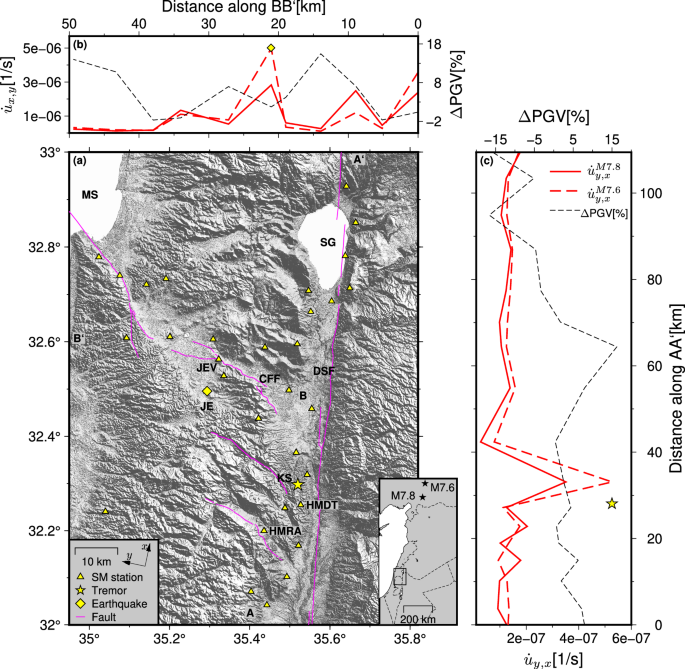
where \({\dot{u}}_{k}^{j}\) and \({\dot{u}}_{k}^{j}\) are the ground velocities in the k direction at station i and J, respectively. To calculate the gradients along the profiles A–A' and B–B' (Figure 1b,c), I first perform band-pass filtering, integrate the accelerations, and rotate the stations to the radial and transverse directions (as indicated by the arrows in the inset in Figure 1a ). I then calculate the gradients between every two adjacent stations using the distance measured along the profile according to equation (3). This results in time series of velocity gradients. For each of these time series, I find the maximum amplitude, bracket it with a window whose length equals 1.5 times the average filter period, and calculate the root mean square (RMS) of the data in the windows. The locations for measuring velocity gradients are taken as the midway distance between the two stations. I apply a series of octave band filters to the velocity gradient time series. Filters range in duration from 128 seconds to 4 seconds. Amplification is observed for up to about 6 seconds. Recall in Fig. 1b, c the frequency ranges in which the ratio between the RMS of MW7.6 and the RMS of MW7.8 is the largest.

Mathematical models LFE-swarm model

The far-field spectral shape is determined by two time scales associated with the function that modulates the LFEs, τe and τs, and by the shape of the source time function, which is determined by the LFE duration τc and the high-frequency decay constant n. Thus the spectra can be expressed as follows:

$$\dot {M}(f)=E(f,{\tau}_{s},{\tau}_{e})\times S(f,{\tau}_{c},n) $$

(4)

Where the function E(f, τs, τe) is responsible for the temporal modulation of the LFEs, and the function S(τc, n) is the time function of the LFE source. Since τs, τc < < τe and τe are generally of a few tens of seconds, the ratio Tr = τs/τc defines the spectral behavior of the tremor source in the frequency range of interest here. In order to simulate the effect of superimposed sources, which can be thought of as a series of LFEs of duration longer than the inter-event time, I set τc equal to 0.5 s, choosing τs from a random set of inter-event times that follow a Poissonian distribution with a scale parameter equal to 0.02 s, and thus It produces about 300 to 500 LFEs per 10 seconds of earthquake. For the poor LFE model, I set the average τs equal to 1 s, which produces about 10 LFEs for every 10 s of earthquake. By setting n = 2, I obtained spectral decay rates of 1 and 2 for the frequency range f < fc وf > fc, respectively. To obtain spectral decay rates proportional to f −3 I combined E with a zero-phase low-pass Butterworth filter whose corner frequency is equal to 0.2 s. I perform 20 iterations, calculate their spectra, and report the average values ​​in Figure 4c.

Dynamic oscillator model

Seismic fault motion is the result of dynamic frictional instability, which requires the friction force to decrease with the accumulated slip or with the slip rate. In addition to having poor slip or velocity, to be able to generate earthquakes, faults must also be frictionally unstable. It is said to be so if its dynamic stiffness is less than a critical value, which can be defined in terms of the slip rate driving the fault. At low slip rates, the critical stiffness is determined by the ratio between the friction force drop and the slip weakening distance. In this system, instability manifests itself as earthquake-like slip events. However, at high slip rates, the critical stiffness increases quadratically with the slip rate, and the failure mode is controlled by inertia. This theory has been supported by laboratory experiments showing that the response of the frictional interface gradually changes with the transition from one regime to another, a phenomenon that has become known as the “slip behavior spectrum.” Numerical modeling shows that rapid stress changes imposed on weak seismic faults will cause them to resonate at certain intrinsic frequencies, thus producing tremor-like signals3. Note that because of the strong dependence on slip rate, any velocity-weakening fault may become unstable if thrust at sufficiently high slip rates. In this study, I simulate tremor spectra by assuming that the loading rate induced by surface waves, which ranges from mm/s to cm/s, places the seismic fault in the inertia-dominated regime. This seems to be a reasonable assumption since the long-term slip rate in the Jordan Valley section of DST is 5 to 6 times lower than the induced surface wave rate. I set the source duration τe to 10 s, and the oscillation period τc to 0.5 s. I dampen the oscillations by exponential multiplication. The duration of the moment acceleration phase τa is 1 and 5 s for the linear and quadratic moment acceleration functions, respectively.

What Are The Main Benefits Of Comparing Car Insurance Quotes Online

LOS ANGELES, CA / ACCESSWIRE / June 24, 2020, / Compare-autoinsurance.Org has launched a new blog post that presents the main benefits of comparing multiple car insurance quotes. For more info and free online quotes, please visit https://compare-autoinsurance.Org/the-advantages-of-comparing-prices-with-car-insurance-quotes-online/ The modern society has numerous technological advantages. One important advantage is the speed at which information is sent and received. With the help of the internet, the shopping habits of many persons have drastically changed. The car insurance industry hasn't remained untouched by these changes. On the internet, drivers can compare insurance prices and find out which sellers have the best offers. View photos The advantages of comparing online car insurance quotes are the following: Online quotes can be obtained from anywhere and at any time. Unlike physical insurance agencies, websites don't have a specific schedule and they are available at any time. Drivers that have busy working schedules, can compare quotes from anywhere and at any time, even at midnight. Multiple choices. Almost all insurance providers, no matter if they are well-known brands or just local insurers, have an online presence. Online quotes will allow policyholders the chance to discover multiple insurance companies and check their prices. Drivers are no longer required to get quotes from just a few known insurance companies. Also, local and regional insurers can provide lower insurance rates for the same services. Accurate insurance estimates. Online quotes can only be accurate if the customers provide accurate and real info about their car models and driving history. Lying about past driving incidents can make the price estimates to be lower, but when dealing with an insurance company lying to them is useless. Usually, insurance companies will do research about a potential customer before granting him coverage. Online quotes can be sorted easily. Although drivers are recommended to not choose a policy just based on its price, drivers can easily sort quotes by insurance price. Using brokerage websites will allow drivers to get quotes from multiple insurers, thus making the comparison faster and easier. For additional info, money-saving tips, and free car insurance quotes, visit https://compare-autoinsurance.Org/ Compare-autoinsurance.Org is an online provider of life, home, health, and auto insurance quotes. This website is unique because it does not simply stick to one kind of insurance provider, but brings the clients the best deals from many different online insurance carriers. In this way, clients have access to offers from multiple carriers all in one place: this website. On this site, customers have access to quotes for insurance plans from various agencies, such as local or nationwide agencies, brand names insurance companies, etc. "Online quotes can easily help drivers obtain better car insurance deals. All they have to do is to complete an online form with accurate and real info, then compare prices", said Russell Rabichev, Marketing Director of Internet Marketing Company. CONTACT: Company Name: Internet Marketing CompanyPerson for contact Name: Gurgu CPhone Number: (818) 359-3898Email: [email protected]: https://compare-autoinsurance.Org/ SOURCE: Compare-autoinsurance.Org View source version on accesswire.Com:https://www.Accesswire.Com/595055/What-Are-The-Main-Benefits-Of-Comparing-Car-Insurance-Quotes-Online View photos