Strength dependence of frequency-magnitude distribution in earthquakes and its implications for the importance of stress state

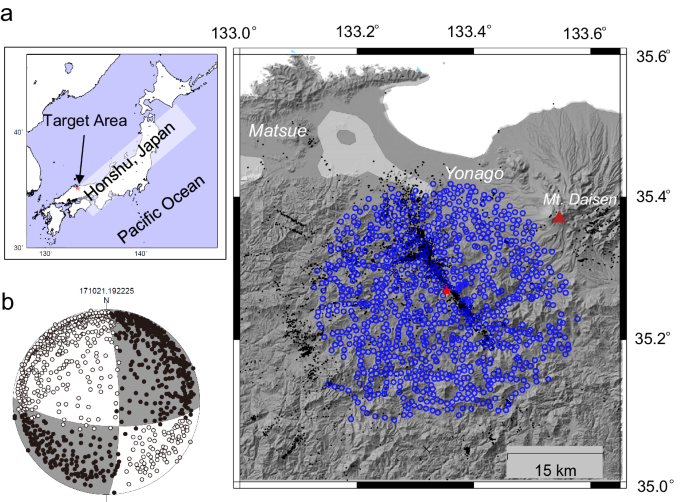
Estimation of the focal mechanism

We determined the deviation of the slip direction from the optimal slip direction expected from the stress field. The study area was divided into spatial bins as shown in Supplementary Figure 2. For the 2017 OBS data, we applied automatic selection and focal mechanism selection processes to continuous seismic records after verifying the data quality of the 100 extracted events by manually comparing the selected results. And the mechanism30. Similar to a previous study, we adopted a depth-dependent smooth velocity structure to determine the center of deficiency. Only events falling within the area covered by the 2017 OBS grid, which contains a total of 3,641 events, were considered. The 2828 events included in the bins are extruded for later analysis. For the year 2000 OBS, we used 2285 events after manually selecting the polarity. The P-axis distributions for both datasets are shown in Supplementary Figure 3 (P-axes for events included in spatial bins where stress field estimation is focused). The focal mechanisms of the selected data were identified using the HASH algorithm. The completeness of detection reached an M value of approximately −0.5 and 1.7 for 2017 and 2000 OBS, respectively, by ZMAP analysis. High quality coordination mechanism solutions were obtained. For each event, the optimal solution was derived as the average tensor from all possible focal mechanism tensors. We also generated 1000 pivot mechanisms for each event based on the solution distribution using HASH. The datasets were used for post-processing. We created 1,000 datasets for FCM solutions by randomly sampling the above 1,000 FCM solutions. This data set was used to calculate the confidence band for the parameters by performing a random sampling. The standard errors of the normal vectors of the decadal levels of events are plotted in Supplementary Figure 4, which reveals average values ​​of 10.8° and 19.8° for 2017 and 2000 in the OBSs, respectively.

field of tension

Normalized deviatoric stress tensors were estimated for the spatial bins. The tensor was derived from seismic moment tensor data for aftershocks, using a method based on the equivalent relationship between inelastic strain and the released seismic moment tensor. We used a stress field estimate using 2017 and 2000 OBS data. We created a moment tensor dataset based on the focal mechanism and magnitude of the earthquake (Ma). The tensor form and scalar moment (M0) were obtained from the estimated focal mechanism and the transformed value of Ma through an empirical relationship used in a previous study: (log(M0) = 1.15 Ma + 10.548). It is worth noting that the estimation of the stress tensor is independent of the choice of error level, because it uses moment tensor data. The stress tensor estimated from seismic data provides a normal tensor form characterized by the principal directions and the ratio between the eigenvalues. Deviated stress tensors were estimated in spatial blocks set at horizontal intervals of 3 km and at a depth of 2.5 km (Supplementary Fig. 2). In addition, we performed the same procedure to distribute the blocks by half a block to the north and east of the origin to smooth the results. The principal directions and relative values ​​of the eigenvectors revealed by the normal skewed stress tensor were estimated from the events that occurred in the spatial box. Concentration mechanism data and estimated parameters in each spatial bin within the 95% confidence interval are shown in Supplementary Data 1. The results obtained using the 2000 OBS data coincide with those using the 2017 OBS data within the 95% confidence interval (Supplementary Figure 5). Therefore, we adopted both datasets to estimate the parameters. The results are consistent with those of previous studies25,26,27. Using both datasets suppressed the confidence band and increased the number of spatial blocks available for subsequent analysis.

Large-resolution parameters were mainly limited to spatial bins around the aftershock zone with relatively high seismic activity. In the subsequent discussion, we focused only on data within spatial bins that show significant precision, as shown in Supplementary Figure 3. The size range adopted for estimating the b value was narrow for the year 2000 OBS (about 1.7 < M < 3.0, which satisfies the GR relationship as Shown in Supplementary Figure 6). Finally, we analyzed 2,155 (1,412 for Mc = -0.3) coordination mechanism data from OBS for the year 2017 to investigate the dependence of the force on the b value.

Supplementary Figure 7 shows a comparison of the number of focal mechanisms with subcenters, including spatial bins, as a frequency-magnitude distribution. The number of focal mechanism data points was slightly smaller than the number of center data points. This difference could be attributed to a less favorable geometric condition of the station distribution or a lower signal-to-noise ratio in the seismograms used to determine the focusing mechanism. The estimated b values ​​show a discrepancy of about 0.07 due to the large variation in the small size range. However, no specific pivotal mechanism has been identified in this data set. Therefore, the relative changes of the value of b on the parts of the Mohr diagram are discussed.

Estimation of shear and normal stress of the stress tensor and selection of crack levels

Normal shear and normal stresses were calculated from the crack geometry and the stress tensor (\({{{{{\boldsymbol{\sigma }}}}}}}\)). According to previous research17, the normal stress vector \({{{{{\boldsymbol{\sigma }}}}}}}_{{{{\bf{N}}}}}}}}\) is the vector product The traction T and the unit error are the normal vector n [\({{{{{{\boldsymbol{\sigma }}}}}}}_{{{{{{\bf{N}}}}}}}=({{{{{\bf{T}}}}}}\cdot {{{{{\bf{n}}}}}}){{{{{\bf{n}}}}}}\)], where the traction vector \(\sigma\) is applied to n; \({{{{\bf{T}}}}}}={{{{\boldsymbol{\sigma }}}}}}{{{{\bf{n}}}}}}\ ). The shear stress vector \({{{{\boldsymbol{\tau }}}}}}\) is expressed as \({{{{{\boldsymbol{\tau }}}}}}={{{{ {\bf{T}}}}}} – {{{{{{\boldsymbol{\sigma }}}}}}_{{{{{\bf{N}}}}}}}\) . From the seismic data (focal mechanism or moment tensor), we can only determine the normal deviatoric stress tensor \(\hat{{{{{{\boldsymbol{\sigma }}}}}}}}\), which is characterized by the main principle directions of eigenvalues The ratio between the eigenvalues. This means that the size of \({{{{{\boldsymbol{\sigma }}}}}}\) is random; Thus, the relative relationship between shear and normal stresses was obtained. In this case, the relationship \({{{{{\boldsymbol{\sigma }}}}}}_{{{{{\rm{N}}}}}}}}}/|{{{ { {\bf{T}}}}}}|{{{{\rm{and}}}}}}{{{{\boldsymbol{\tau }}}}}}/|{{{{ {\bf {T}}}}}}|\) of \(\hat{{{{{\boldsymbol{\sigma }}}}}}}}\) and n. Therefore, we can define Mohr's circle in terms of its diameter, with its center point at the origin of the coordinates. For example, the maximum shear stress under a stress tensor acting on a plane with a normal vector rotated at 45° from the maximum principal direction to the lowest principal direction of the stress tensor is plotted at (normal stress, shear stress) = (0), 1) on Natural circle (unit) of Mohr. In this study, we used coordinates to express location on Mohr's circle by r (radial length from the center, i.e., ranging from 0 to 1) and θ (clockwise angle from the horizontal).

To estimate the normal and shear stresses on a unit Mohr circle, a normal error vector is required. We have two normal vector candidates for each event from the focal mechanism solution since there are two nodal planes. The following chart was used to select one of the two aircraft. First, we removed the crack plane if it had an inappropriate angle (dθ), which is the discrepancy between the slip vector of the focusing mechanism and the maximum shear stress direction expected from the stress field, which exceeds 30°. We set two conditions for choosing the error level: (1) misfit angle (dθ) and (2) comparison of the section lengths (dp) with the line defined by the CFF for a given two-point friction coefficient \(\mu )\) calculated by the normal vectors of the candidates. A schematic diagram of this process is shown in Supplementary Figure 8. The shear force in CFF is expressed in (1) and \(p\propto {{{{{\rm{d}}}}}}}p\) represents the relationship to which the pressure is proportional Pore ​​fluid p with dp, respectively. The point touching the CFF line on the Mohr unit circle with angle θc can be expressed by \({\theta }_{c}={\tan }^{-1}(1/\mu )\), as shown in the figure Supplementary 8b and reported by Geiger et al. Unfavorable crack levels for the stress field require a high value of p to generate rupture, which is more difficult to achieve naturally than in situations with low p, due to difficulties in maintaining high p.

The range of dθ was calculated for each level of the pressure field within a 95% confidence interval in the spatial bin containing the event. First, we chose a level with a smaller dθ range than the other level (Condition 1). However, if the dθ ranges overlapped, we chose a level with a smaller dp (condition 2). This criterion is known as selection based on error nonstationarity, as defined in a previous study. To calculate dp, we set μ = 0.6, which is a typical internal friction coefficient. However, assuming μ = 0.2 or 1.0 did not change the result (Supplementary Figure 9).

After completing the above process for each event, we compared the specific crack plane of the estimated stress tensor with that of another event. As shown in the stress field section, the spatial mass distribution shifted to half the mass size horizontally, meaning that there are stress field candidates for most events. We used a fault plane and stress field combination that provides a relatively small misfit dθ.

B- Estimating the value

The b value, which represents the power law decay of the frequency-magnitude distribution, is estimated in different regions and shows spatial and temporal variations. We followed the standard method (i.e. maximum likelihood method) to estimate the b value38,39,40. We assigned a fixed size range (minimum and maximum size) to each part of Mohr's circle, as comparing b values ​​across different parts of the circle is crucial to this study. We used a size range of −0.3 to 2, with the lower limit determined using the ZMAP program. The upper limit is set at a position where the portion of the frequency-magnitude relationship deviates slightly from the linear relationship between log N and M (i.e., away from the Gutenberg-Richter relationship). In addition, the number of earthquakes above the upper limit was too small to analyze the b-value variation within the Mohr circle.

We estimated b values ​​for parts of the Mohr Circle containing more than 50 events, excluding events near the coseismic fault of the 2000 West Tottori Earthquake. Inhomogeneity of the stress field may lead to an incorrect estimate of the fault direction relative to the stress field. Based on the co-seismic fault model, we calculated the distance to fault planes and selected events that were located further than a certain distance (R). In this study, we set R = 0.5 km. The results for different distance settings are shown in Supplementary Figure 10a. Increasing R resulted in a significant reduction in the number of usable events due to the concentration of downcenters around co-seismic fault planes (Supplementary Fig. 10b). The number of excluded events with larger mismatches, as shown in the previous section, decreased as R increased, indicating the influence of near misses on the events. We chose R = 0.5 km, which resulted in 65% of events from the initial set being used, while 8% were excluded.

The Mohr unit circle was divided into parts expressed in terms (r minimum, r maximum; θ° minimum, θ° maximum) in the coordinates shown in the inset of Figure 2(c); The ranges are (0.8, 1, 10, 30), (0.8, 1, 20, 40), (0.8, 1, 40, 60), (0.8, 1, 60, 80), (0.8, 1, 70, 90 ), (0.8, 1; 80, 100), (0.8, 1, 90, 110), (0.5, 0.8, 22.5, 67.5), (0.5, 0.8, 45, 90), (0.5, 0.8, 67.7, 112.5 ), (0, 0.8, 0, 90), and (0, 0.8, 90, 180). The mean and median values ​​of the standard error between events belonging to each part r and θ are listed in Supplementary Table 2. Errors in r and θ were calculated from the ideal focal mechanism data set and 1000 and the stress field estimated by the bootstrap random sampling procedure. Although the error range of θ became larger than that of r, the division in Mohr's circle was sufficient to capture the characteristic of the b-value distribution.

What Are The Main Benefits Of Comparing Car Insurance Quotes Online

LOS ANGELES, CA / ACCESSWIRE / June 24, 2020, / Compare-autoinsurance.Org has launched a new blog post that presents the main benefits of comparing multiple car insurance quotes. For more info and free online quotes, please visit https://compare-autoinsurance.Org/the-advantages-of-comparing-prices-with-car-insurance-quotes-online/ The modern society has numerous technological advantages. One important advantage is the speed at which information is sent and received. With the help of the internet, the shopping habits of many persons have drastically changed. The car insurance industry hasn't remained untouched by these changes. On the internet, drivers can compare insurance prices and find out which sellers have the best offers. View photos The advantages of comparing online car insurance quotes are the following: Online quotes can be obtained from anywhere and at any time. Unlike physical insurance agencies, websites don't have a specific schedule and they are available at any time. Drivers that have busy working schedules, can compare quotes from anywhere and at any time, even at midnight. Multiple choices. Almost all insurance providers, no matter if they are well-known brands or just local insurers, have an online presence. Online quotes will allow policyholders the chance to discover multiple insurance companies and check their prices. Drivers are no longer required to get quotes from just a few known insurance companies. Also, local and regional insurers can provide lower insurance rates for the same services. Accurate insurance estimates. Online quotes can only be accurate if the customers provide accurate and real info about their car models and driving history. Lying about past driving incidents can make the price estimates to be lower, but when dealing with an insurance company lying to them is useless. Usually, insurance companies will do research about a potential customer before granting him coverage. Online quotes can be sorted easily. Although drivers are recommended to not choose a policy just based on its price, drivers can easily sort quotes by insurance price. Using brokerage websites will allow drivers to get quotes from multiple insurers, thus making the comparison faster and easier. For additional info, money-saving tips, and free car insurance quotes, visit https://compare-autoinsurance.Org/ Compare-autoinsurance.Org is an online provider of life, home, health, and auto insurance quotes. This website is unique because it does not simply stick to one kind of insurance provider, but brings the clients the best deals from many different online insurance carriers. In this way, clients have access to offers from multiple carriers all in one place: this website. On this site, customers have access to quotes for insurance plans from various agencies, such as local or nationwide agencies, brand names insurance companies, etc. "Online quotes can easily help drivers obtain better car insurance deals. All they have to do is to complete an online form with accurate and real info, then compare prices", said Russell Rabichev, Marketing Director of Internet Marketing Company. CONTACT: Company Name: Internet Marketing CompanyPerson for contact Name: Gurgu CPhone Number: (818) 359-3898Email: [email protected]: https://compare-autoinsurance.Org/ SOURCE: Compare-autoinsurance.Org View source version on accesswire.Com:https://www.Accesswire.Com/595055/What-Are-The-Main-Benefits-Of-Comparing-Car-Insurance-Quotes-Online View photos