Support vector regression model to predict the maximum seismic response of buildings based on real observation data

Training and testing results of the SVR-MDR model

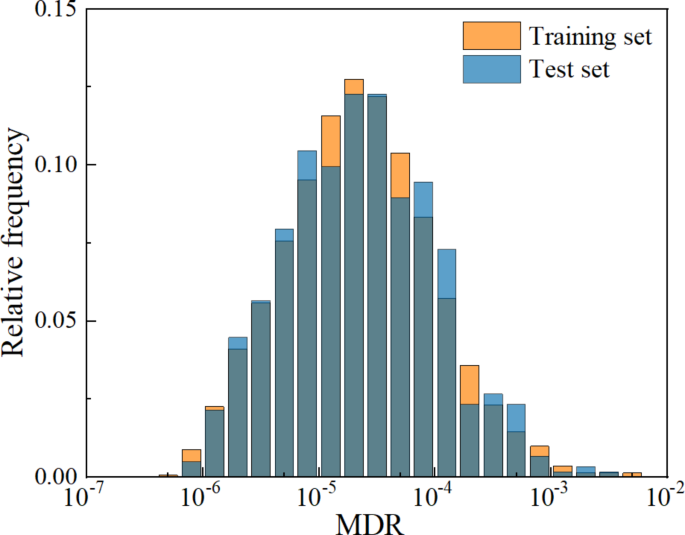
In this section, the seismic response data of SRC buildings in NDE1.0 are used to train the SVR-MDR model. MDR was chosen as the target output of the model, and 41 parameters including 6 structural information parameters, 9 spectrum information parameters, 16 duration information parameters, and 10 other seismic information parameters were selected as input feature. The training and testing datasets are split 9:1 using the StandardScaler function in scikit-Learn, a free and open source machine learning library for Python. Figure 1 shows the normal probability distribution of MDRs on the training and testing datasets. It shows that the test data set has almost the same distribution as the training data set.

Figure 1

Normal probability distribution of MDR on training and testing dataset.

Four criteria are presented to evaluate the predictive performance of the SVR model, including the standard deviation of error (\(\:\sigma\:),\:\:\)mean absolute relative deviation (MARD) and the coefficient of determination (\(\:{R} ^{2}\)) and the fraction of a data set whose relative difference is no more than 10% (\(\:{D}_{10\%}\)). The MARD expressions, \(\:{R}^{2}\), \(\:{D}_{10\%}\) are given by

$$\:\begin{array}{c}MARD=median\left(\left|\frac{{\widehat{y}}_{i}-{y}_{i}}{{y}_{ i}}\right|\right)\end{array}$$

(13)

where \(\:{\widehat{y}}_{i}\) is the expected value, and \(\:{y}_{i}\) is the corresponding true value;

$$\:\begin{array}{c}{R}^{2}=1-\frac{{\sum\:}_{i=1}^{n}{\left({\widehat{y) }}_{i}-{y}_ {i}\right)}^{2}}{{\sum\:}_{i=1}^{n}{\left({y}_{i}-\stackrel{-}{)r} \right)}^{2}} \end{array}$$

(14)

where \(\:\stackrel{-}{y}\) is the average of \(\:{y}_{i}\). MARD indicates the central tendency of errors. It measures how well the expected value matches the real value. The value of \(\:{R}^{2}\) is used to determine the goodness of fit of the model, the best possible score for \(\:{R}^{2}\) is 1.0 and it can be negative when the model is arbitrarily worse . A high value of \(\:{R}^{2}\) indicates a good fitting effect of the model.

$$\:\begin {array} {c} {{\updelta \:}}_{i} = \frac {{y}_{i} – {\widehat {y}}_{i}} {{ y}_{i}}\times\:100\% \end{array}$$

(15)

The above expression for \(\:{\delta\:}_{i}\) represents the normalized error between the predicted value and the true value of the sample point in the test set. \(\:{D}_{10\%}\) is the percentage of sample points that \(\:{\delta\:}_{i}\:\) lies in the range [− 10%, 10%]. To obtain the best SVR model, the hyperparameters (C, γ) of the Gaussian kernel are determined using grid search and 10-fold cross-validation. n-fold cross-validation divides the training data set into exclusive, complementary, and complementary subsets. Each time, it uses n-1 subsets as the training set and the remaining subset as the test set. The optimal hyperparameters are determined by selecting the model that gives the minimum mean error. Mean squared (MSE) for all n subsets.

The predictive performance of the training and testing datasets is shown in Fig. 2a, b. The 1:1 solid line represents that the predicted value equals the true value, and the dashed red lines represent one standard deviation. The prediction model generally approaches a 1:1 linear proportional relationship. The standard deviation of errors on the training and testing dataset is 0.181 and 0.202, respectively. The calculated \(\:{D}_{10\%}\) for the training and testing datasets are 97.1% and 91.2%, respectively, which indicates that the SVR-MDR model has high accuracy in predicting MDR.

Figure 2

Distribution of predicted and true MDR using SVR-MDR model with all 41 input features (a) Training dataset; (b) Test data set.

The performance of the SVR-MDR model is compared with two other machine learning models: kernel series regression (KRR) and decision tree (DT). A radial basis function kernel is used in KRR and the hyperparameters are chosen as α = 1, γ = 0.01, and the maximum depth of the decision tree is 10. The results of the KRR model and the DT model for the training and testing sets are shown in Figs. 3 and 4 respectively. The predictive performance metrics of SVR-MDR, KRR, and decision tree are shown in Table 4. The KRR model shows greater variance, especially when predicting larger MDRs, indicating lower prediction accuracy than our SVR-MDR model. Although the DT model shows a much smaller dispersion, the large difference between the standard deviations of prediction error for the training and test sets indicates possible overfitting. In comparison, the SVR-MDR model not only shows superior predictive accuracy but also maintains greater stability in both training and test sets, highlighting better performance in MDR prediction compared to the KRR and DT models.

Figure 3

Distribution of predicted and true MDR using KRR model with all 41 input features (a) Training dataset; (b) Test data set.

Figure 4

Distribution of predicted and true MDR using DT model with all 41 input features (a) Training dataset; (b) Test data set.

Table 4: Predictive performance measures of SVR-MDR, KRR, and DT. Training and testing results of the RSVR-MDR model

There are 41 input features in the SVR-MDR prototype, and each feature exerts different degrees of influence on the performance of SVR-MDR. To measure the importance of each feature, the SHAP method proposed by Lundberg and Lee is used. SHAP is a machine learning annotation tool that aims to evaluate the impact of each feature. It uses the Shapley value as an evaluation index, which reflects the average change in prediction results when a given feature is added to all possible combinations of other features. Due to the relatively high computational cost of implementing SHAP for SVR-MDR, 604 data sets, about 10% of the total SRC earthquake response data, were randomly selected. The absolute SHAP values ​​for each feature in these 604 samples are arranged as shown in Figure 5.

Figure 5

SHAP values ​​for 41 input features: (a) structural information; (b) other information about earthquakes; (c) spectrum information; (d) Duration information.

The fundamental frequency f1 and the combined seismic minimum frequency f2 contribute significantly to the prediction in the six structural information parameters. Size, with the highest SHAP value of 85.71, contributes significantly to the prediction, indicating a dominant effect of size on MDR prediction. In the spectral information parameters, the average pseudo-spectral acceleration (Avg_Sa) between the fundamental frequency f1 and the common minimum seismic frequency f2 contributes significantly to the prediction. DSa2, the duration corresponding to (5-95)% of the total energy associated with ground motion acceleration, contributes significantly to the prediction in the 16 duration information parameters. It should be noted that the input feature selection should not only be based on the SHAP value ratings, but also On the practical availability of the input feature. For example, although the fundamental frequency f1 has a lower SHAP value than the minimum common seismic frequency f2, f1 is more accessible than f2. Since the former can be easily obtained by empirical formula or model analysis; On the other hand, F2 requires the construction of response records under a specific ground motion. Therefore, the minimum co-seismic frequency and dependent parameters, such as SA2, SV2, SD2, Avg_Sa, Avg_Sv, and Avg_Sd, cannot be easily obtained after the earthquake and are not considered in the reduced SVR model. A total of 10 input features were finally selected based on their importance and ease of acquisition, including 3 building information parameters (structure height H, number of stories N, fundamental frequency f1), and 4 other seismic information parameters PGV, PGD, central distance Dep and magnitude M, and 3 spectrum information parameters SA1, SV1, SD1. The RSVR-MDR model is then trained using these 10 input features. The predictive performance of the RSVR-MDR model is shown in Figure 6. The standard deviation of errors on the training and testing dataset are 0.192 and 0.213 respectively, which is almost the same as that of the SVR-MDR model. The calculated \(\:{D}_{10\%}\) for the training and testing datasets is 97.0% and 95.7%, respectively, which are almost the same as that of the SVR-MDR model. In this regard, the RSVR-MDR with 10 features (H, N, f1, PGV, PGD, Dep, M, SA1, SV1, SD1) has almost the same predictive performance as the SVR-MDR model with all 41 features. It is worth noting It is noted that although the duration information parameters DSa2 and DSv2 have a higher SHAP value than the building information parameters such as structural height H and number of stories N, the corresponding predictive performance with 10 features (DSa2, DSv2, f1, PGV, PGD, Dep, M, SA1, SV1, SD1) is worse than that with 10 features (H, N, f1, PGV, PGD, Dep, M, SA1, SV1, SD1 ), as shown in Figure 7. In this regard, in the multi-feature set, the building information parameters are more important than the duration information parameters.

Figure 6

Distribution of predicted and true MDR using RSVR-MDR with 10 selected input features (H, N, f1, PGV, PGD, Dep, M, SA1, SV1, SD1) (a) Training dataset; (b) Test data set.

Figure 7

Predicted and true MDR distribution using RSVR-MDR with 10 selected input features (DSa2, DSv2, f1, PGV, PGD, Dep, M, SA1, SV1, SD1) (a) Training dataset; (b) Test data set.

What Are The Main Benefits Of Comparing Car Insurance Quotes Online

LOS ANGELES, CA / ACCESSWIRE / June 24, 2020, / Compare-autoinsurance.Org has launched a new blog post that presents the main benefits of comparing multiple car insurance quotes. For more info and free online quotes, please visit https://compare-autoinsurance.Org/the-advantages-of-comparing-prices-with-car-insurance-quotes-online/ The modern society has numerous technological advantages. One important advantage is the speed at which information is sent and received. With the help of the internet, the shopping habits of many persons have drastically changed. The car insurance industry hasn't remained untouched by these changes. On the internet, drivers can compare insurance prices and find out which sellers have the best offers. View photos The advantages of comparing online car insurance quotes are the following: Online quotes can be obtained from anywhere and at any time. Unlike physical insurance agencies, websites don't have a specific schedule and they are available at any time. Drivers that have busy working schedules, can compare quotes from anywhere and at any time, even at midnight. Multiple choices. Almost all insurance providers, no matter if they are well-known brands or just local insurers, have an online presence. Online quotes will allow policyholders the chance to discover multiple insurance companies and check their prices. Drivers are no longer required to get quotes from just a few known insurance companies. Also, local and regional insurers can provide lower insurance rates for the same services. Accurate insurance estimates. Online quotes can only be accurate if the customers provide accurate and real info about their car models and driving history. Lying about past driving incidents can make the price estimates to be lower, but when dealing with an insurance company lying to them is useless. Usually, insurance companies will do research about a potential customer before granting him coverage. Online quotes can be sorted easily. Although drivers are recommended to not choose a policy just based on its price, drivers can easily sort quotes by insurance price. Using brokerage websites will allow drivers to get quotes from multiple insurers, thus making the comparison faster and easier. For additional info, money-saving tips, and free car insurance quotes, visit https://compare-autoinsurance.Org/ Compare-autoinsurance.Org is an online provider of life, home, health, and auto insurance quotes. This website is unique because it does not simply stick to one kind of insurance provider, but brings the clients the best deals from many different online insurance carriers. In this way, clients have access to offers from multiple carriers all in one place: this website. On this site, customers have access to quotes for insurance plans from various agencies, such as local or nationwide agencies, brand names insurance companies, etc. "Online quotes can easily help drivers obtain better car insurance deals. All they have to do is to complete an online form with accurate and real info, then compare prices", said Russell Rabichev, Marketing Director of Internet Marketing Company. CONTACT: Company Name: Internet Marketing CompanyPerson for contact Name: Gurgu CPhone Number: (818) 359-3898Email: [email protected]: https://compare-autoinsurance.Org/ SOURCE: Compare-autoinsurance.Org View source version on accesswire.Com:https://www.Accesswire.Com/595055/What-Are-The-Main-Benefits-Of-Comparing-Car-Insurance-Quotes-Online View photos